一些有趣的问题以及我的思考

三门问题

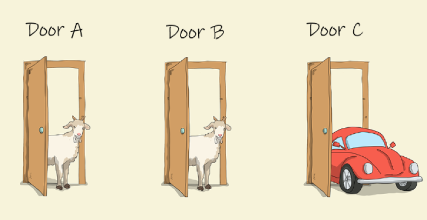
假设你正在参加一个游戏节目，你被要求在三扇门中选择一扇：其中一扇后面有一辆车；其余两扇后面则是山羊。你选择了一道门，假设是一号门，然后知道所有门后面有什么的主持人，开启了另两扇中 其中一扇后面有山羊的门，假设是三号门。他然后问你：“你想选择二号门吗？”变换你的选择对你来说是一种优势吗？

疑惑不解：我根本不知道这些门后面是什么，换不换的有啥区别么？概率究竟是怎么被新增加的信息所影响的？

一语中的：变换选择实际上相当于选择了两扇门。

刨根问底：选择的这两扇门中至少有一只山羊，主持人不过是把那只山羊提前展示出来罢了，故获胜概率从 1/3 提升到了 2/3。

1 千克水能不能浮起 2 千克木头？

疑惑不解：浮力不是排开水的重量吗？水好像不太够吧。

一语中的：把“排开”理解为“替换”。

刨根问底：想象一下，把水池中任意区域的 2 千克的水替换成木头，这个木头受到的浮力就是原来水受到的浮力（相当于只改变了内部结构，不影响整体受力），我们假定木头的密度小于等于水，那木头的质量也就小于等于之前的水，所以可以漂浮起来。注意，替换的水不用再倒回水池，而水池里剩余的水，按照简单的数学模型，只要大于 0 就可以了（当然，现实中水分子的粒度不是无限小）。

为什么镜子里面左右相反，而上下关系却相同？

疑惑不解：左右和上下不是等价的吗？是什么导致左右的特殊性？

一语中的：是我们不自觉中把它转换成了左右对称来理解。

刨根问底：看上面的小熊，当我们去对比空间中两个相似的物体时，一定会通过旋换去统一它们的上下和前后方向，然后再进行对比，这是一个自然演化出的高效的识别策略。不管定义哪个角度是物体的正面，在已经锁定两个坐标轴方向的前提下，互为镜像的两个物体只能转换为按照第三个坐标轴方向对称，也就是左右关系。

硬币悖论

事实上与我的直觉相符，所以在这里不做过多讨论，仅作纪念收藏。

第一次看到这个问题应该是在“真理元素”那里，我以为会很有趣，会反直觉。事实上他那个视频也确实有趣，不过是在后面的扩展部分，比如在图形内部滚动就是 N - 1 而不是 N + 1，因为自转方向与曲线弯曲方向相反。在视频的后面还扩展到了恒星年与回归年的关系。

重力加速度约等于圆周率的平方，是巧合吗？

疑惑不解：这俩完全是八竿子打不着吧，况且其中一个还是纯数学常量。

一语中的：如果长度单位是基于重力加速度定义的话（却有此定义，但不是原始定义），后者为一个简洁常数很正常。

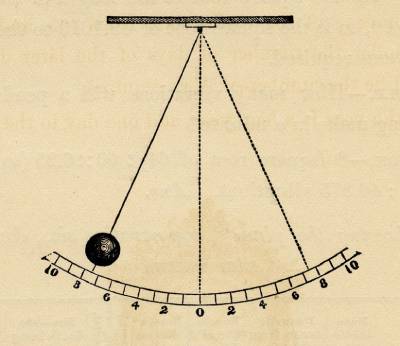
刨根问底：根据单摆的近似周期公式（严格值需要用级数表示）g = (4 * L * pi^2) / T^2（其中，g 为重力加速度，T 为单摆周期，pi 为圆周率，L 为摆长），如果我们定义使得周期为 2s 时，对应的摆长称为 1m，则有 g = pi^2 * (m / s^2)，即重力加速度为 pi^2 个单位。历史上确实出现过这样用秒摆来定义“米”的方案，如果米的最初来源就是这里，那可以说这不是巧合。但就如同法国国民议会基于子午线长度来定义“米”一样，它们都只是在拟合一个早已存在的长度单位——半“突阿斯”(toise)。所以，这确实只是个巧合，正如地球的子午线刚好接近 4 万公里一样。